数组是存放相同类型数据的集合
数组有两个基本要求:
- 存放的数据类型必须相同
- 必须有一个或多个元素
数组是一种c语言中的自定义类型,也是大部分c语言学习者最早接触到的自定义类型
一维数组的创建语法如下:
- : 数组元素的数据类型,可以是任意有效的类型
- : 数组的名字,遵循标识符命名规则
- : 指定数组的长度,即元素的个数,必须是一个常量表达式,不能使用变量
举个例子,下面的代码创建了一个名为的数组,用于存放5个学生的成绩:
这行代码定义了一个数组变量,它可以存储5个类型的元素。
仅仅创建数组,只是在内存中划分了一块连续的空间,数组中的元素还没有确定的值。为了给数组中的元素赋初值,需要在创建数组的同时对它进行初始化。
完全初始化:
完全初始化是指在创建数组时,为数组的每个元素都指定初始值。例如:
在数组名后面加一个赋值号,然后在大括号中列出全部元素的初始值,这就完成了数组的完全初始化。
需要注意的是,初始值的个数不能超过数组的长度。如果初始值的个数小于数组长度,剩余的元素会被自动初始化为0。
不完全初始化
如果在初始化数组时,只为部分元素指定初始值,这种初始化方式称为不完全初始化。例如:
上述代码创建了一个长度为5的数组,但只为前3个元素指定了初始值。对于未显式初始化的元素,编译器会自动将其初始化为0。因此,上述数组初始化后的完整值为。
数组也是有类型的,数组的类型由两部分组成:
- 元素的类型
- 数组的长度
可以用的形式来表示数组类型。例如:
- :表示一个由5个类型元素组成的数组
- :表示一个由10个类型元素组成的数组
数组的类型决定了数组占用内存空间的大小。对于类型的数组,每个元素占用4个字节,数组的长度为5,因此整个数组占用个字节。
需要注意的是,两个元素类型相同但长度不同的数组,它们的类型是不同的。比如和是两种不同的类型。
创建并初始化数组后,我们就可以使用数组了。数组最常见的操作就是访问其中的元素,可以读取元素的值,也可以修改元素的值。
C语言规定,数组的每个元素都有一个编号,称为数组的下标或索引。下标从0开始,第1个元素的下标为0,第2个元素的下标为1,以此类推。
访问数组元素的语法格式为:
举个例子:
通过数组名和下标,我们可以访问数组中的任意一个元素。需要注意以下几点:
- 下标必须是整数类型,可以是整型常量、变量或表达式
- 下标的取值范围是0到数组长度-1,如果下标越界,会导致未定义的行为
以上讲述的都是数组的基本语法,接下来从内存出发,理解数组的本质。
当使用,就是创建了一个名为的变量,变量类型为。
变量类型会决定这个变量在内存中开辟多少空间,此处变量类型为,那么就是在内存中开辟5个类型大小的空间。然后依次在五个空间内存入五个数据。
依次打印五个数组元素的地址:

可以发现,每个元素相比于上一个元素地址大四个字节,可是这种变量是在栈区开辟的空间,栈区内存是从高到低使用的,难道不应该每个元素的地址相比于上一个元素小四个字节吗?
在创建一维数组时,数组类型确定,就可以确定这个数组占用的总大小。因为数组类型是,元素类型决定一个元素的大小,数组长度决定元素的个数,依据这两者,就可以知道数组的总大小。
比如以上代码,对于栈区的三个变量、、,它们的地址依次变低,因为栈区地址从高到低分配,这并不破坏规则。通过数组类型,可以得知整个数组占用,那么内存就会分配这么多空间给数组,在数组内部如何使用这些空间,内存并不关心。
也就是说,栈区内存分配依然是从高到低的,整个数组空间是一次性分配的,只是数组内部是从低到高使用的。
在数组内部,c语言规定下标从小到大,数组元素地址也是从小到大的,为什么要这样设计?
因为数组的访问本质上是指针对地址的访问,接下来用几个例子来证明:

通过以上代码,主要是证明、、三者值相同,都是数组首个元素的地址。

此处和访问到的结果一样,说明本质上就是对从地址开始,偏移量为个的地址进行访问,而和等价,都是首个元素的地址。
而当偏移量为正数,偏移后地址是变大的,也就是说在内存中要保证后面的元素地址比前面的元素大,才能用指针偏移量来访问,否则用负数的指针偏移量访问不是很别扭吗?
在此还能解释一个问题:为什么数组下标要从开始?
当访问第一个元素,本质上来说就是,也就是访问地址本身,即第一个元素的地址。如果下标从开始,那在那么在利用指针访问时就要对所有地址,反而麻烦,于是一开始就规定下标从0开始,后续直接利用下标作为偏移量就行了。

如果把一维数组比作一条线,那么二维数组就像一个矩形,多了一个维度,引入了"行"和"列"的概念。
二维数组的定义形式为:
该定义创建了一个名为的二维数组,其中:
- :数组元素的数据类型
- :数组的行数
- :数组的列数
例如:
上述代码定义了一个名为的二维数组,该数组有3行4列,共12个元素,每个元素的类型为。
需要注意的是,数组的行数和列数都必须是常量表达式,不能使用变量。
和一维数组一样,二维数组如果在定义时没有显式初始化,那么数组中的元素值是不确定的。为了给数组中的元素赋予初值,可以在定义数组的同时进行初始化。
逐个元素初始化
最直观的初始化方式是为每个元素逐个赋值,例如:
上述代码创建了一个2行3列的二维数组,并按照行优先的顺序依次为每个元素赋值。这种初始化方式要求初始值的个数与数组元素的总数一致。
按行初始化
更常见的初始化方式是按照行来组织初始值,每行数据用一对大括号括起来,例如:
按行初始化的好处是结构清晰,一眼就能看出数组的行列结构。
部分初始化
和一维数组类似,如果初始值的个数小于数组元素总数,那么未被初始化的元素会被自动初始化为0。例如:
上述代码只显式初始化了第一行的前两个元素和第二行的第一个元素,其余元素都会被初始化为0。因此,该数组初始化后的完整值为:

一维数组的下标从0开始依次递增。对于二维数组,行与列各有一组下标,分别从0开始递增。
在平面直角坐标系中,只要确定了和就能确定一个点,相同的,二维数组中只要确定了行和列的下标,就可以确定一个元素。
那么如何通过两个下标访问一个二维数组的元素?在此需要用到两个下标访问操作符,分别确定行列的下标。
如在数组中找到2行3列的元素:
二维数组的结构
一维数组访问的本质是通过首元素地址与偏移量来访问一个地址。其实二维数组也是通过首元素的地址与偏移量来访问的。
但是一个数组元素只有一个地址,一个偏移量就可以锁定元素了,为何需要两个偏移量?
尝试输出一个二维数组的所有元素地址:
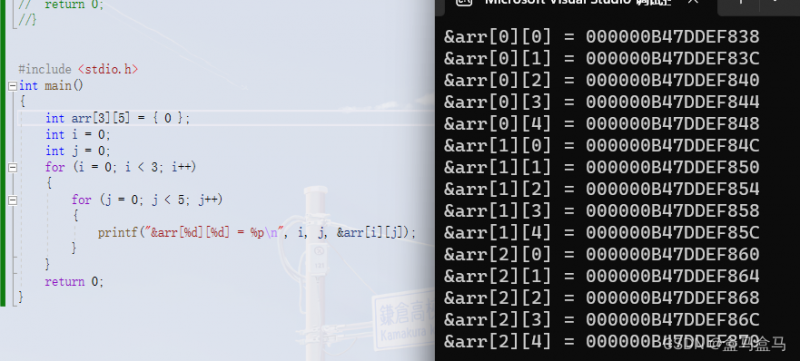
可以发现,每两个元素之间的差值都是字节,也就是一个的内存大小。二维数组并非想象中那样是一个平面,而是一个连续的地址:

其实二维数组可以理解为两层数组,外层数组用于存放一维数组,内层数组用于存放元素。
也许有点难以理解这句话,拿例子来分析:


上图中,有三个基本的数组,每个数组存放5个元素。而在下方有一个存放了三个数组的外层数组。可以发现,通过利用外层数组名来访问,可以正常得到每个元素。那么这样的数组形式是如何访问到每个元素的呢?
首先理清几个概念:
- 外层数组也是数组,但是外层数组的元素是数组
- 外层数组的数组名本质上也是一个指针,与一维数组相同
- 对指针解引用,得到的是外层数组的第个元素,但是此元素是一个数组,数组名本质上是指针,所以 得到的是一个指针
如果理解了以上三点,说明对数组和指针掌握的还不错。访问二维数组使用首元素地址和两个下标,也就是,在讲解一维数组本质的时候提到过:
那么连续使用两个,其实就是解引用了两次:
那么为什么一维数组解引用一次就得到了目标值,二维数组要解引用两次?
在理清概念时提起过,外层数组的变量是指针,得到的是一个指针。对于这样一个指针,仍然可以使用偏移量与解引用操作符去访问,。将此处的指针替换为, 那么最后的表达式就是刚才的表达式。
再用代码证明一次:

确实可以通过这样的一个表达式访问到二维数组的所有元素。
进一步对ij两个偏移量解析:
指针是有步长的,类型的指针的步长是字节,类型指针步长为字节。那么数组指针的步长是多少?答案是不确定的,这个数组占用的空间是多大,这个类型的数组指针步长就是多大。
- 在一维数组中,数组名的本质就是首个元素的指针,此指针的步长是一个元素占用的内存
- 在二维数组中,数组名的本质也是首个元素的指针,但是此处首元素是一维数组,故此指针的步长是此一维数组的所有元素占用的内存
利用以下代码证明:

在一开始创建了一个行为,列为的数组,可以将此二维数组拆成三个一维数组,每个数组有个元素,大小是字节。
在上述指针的加减法中,偏移了个字节的地址,偏移了个字节的地址。可以发现,刚好分别就是一个数组的大小与两个数组的大小。这就可以说明,此处的是一个指针,且指针类型是数组指针。
其实等效于,但是与不等效,这三者的数值都是一样的,但是和是数组指针,是普通的指针。
解析一下二维数组访问表达式中与造成了的偏移:

刚刚辨析过,外层数组的元素类型是数组指针,指针在偏移时偏移量是:这个指针指向的元素的大小。
对于外层数组,面对的是一个步长为字节的指针,所以会导致指针跳过个字节。从上图中也可以看出,每自增,指针就跳过了五个元素。
对于内层数组,此时一个元素就是一个的大小,作为内层数组的偏移量,每次自增造成的偏移量也就是个元素了。
二维数组通过这样的对指针步长的运用,一个用于跳过数组,一个用于跳过元素,造成了一个“二维”的假象。
在C99标准之前,C语言在创建数组的时候,数组大小的指定只能使用常量、常量表达式省略数组大小。
比如以下三种方式,得到的数组都是固定的大小:
这样的语法限制,创建数组就不够灵活,有时候数组大了浪费空间,有时候数组又小了不够用。
中新增了变长数组(,简称 )的新特性,允许使用变量指定数组大小。
上面示例中,数组 就是变长数组,因为它的长度取决于变量 的值,编译器没法事先确定,只有运行时才能知道 是多少。
变长数组的根本特征,就是数组长度只有运行时才能确定,所以变长数组不能初始化。它的好处是程序员不必在开发时,随意为数组指定一个估计的长度,而是在运行时为数组分配精确的长度。
变长数组的意思是数组的大小是可以使用变量来指定的,在程序运行的时候,根据变量的大小来指定数组的元素个数,而不是说数组的大小是可变的。数组的大小一旦确定就不能再变化了。
柔性数组也是在标准后才出现的,它是指:对于动态内存中的结构体的最后一个成员,可以放一个长度可以改变的数组。
创建柔性数组语法如下:
柔性数组定义时,需要定义在一个结构体的尾部,数组的内部,可以不填值,或者填入。注意:部分编译器只支持其中一种写法。
在以上代码中,都在结构体末尾放了一个数组,此数组的内部没有值或者值为。这就是柔性数组的基本语法,若数组不是最后一个成员,或者数组内有以外的值,最后创建的都不是柔性数组,而是定长数组。
柔性数组有以下特性:
- 柔性数组成员前至少有一个其它成员
- 计算结构体的大小时,不计入柔性数组成员
- 柔性数组的长度变化由与决定,在第一次使用开辟内存时,必须大于结构体其它成员占用内总和,多出来的内存分配给柔性数组。
为了理解这些特性以及柔性数组的长度变化,分析一串代码:
柔性数组开辟:
一开始创建了一个结构体,在利用动态内存开辟了属于结构体本身的空间后,追加了个类型的大小,用于存放柔性数组的元素。
此处也利用了不计算柔性数组的特性,避免程序员自己计算结构体的大小,追加的空间也更加直观。
柔性数组增长:
上述代码在开辟了个元素的空间后,仍需要空间放其它元素,于是使用开辟了额外的五个空间,这就是柔性数组的长度变化。
